Теперь рассмотрим схемы графиков многочленов четвёртой степени 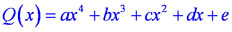 .
.
Заметим, что как при больших отрицательных, так и при больших положительных значениях аргумента x
значения функции будут большими числами, совпадающими по знаку с коэффициентом a . Пусть коэффициент
1 случай.
Производная многочлена 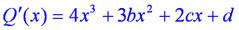 имеет три различных корня
x1 , x2 ,
x3.
имеет три различных корня
x1 , x2 ,
x3.
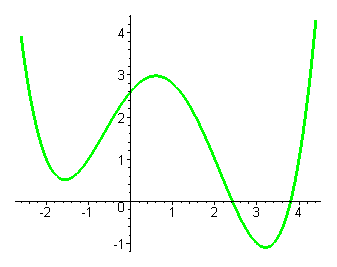
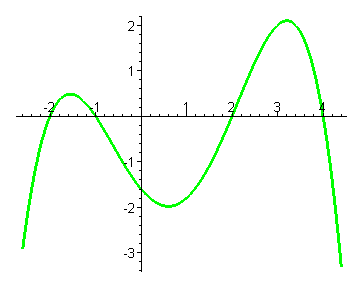
| В этом случае функция имеет три точки экстремума и график выглядит следующим образом. |
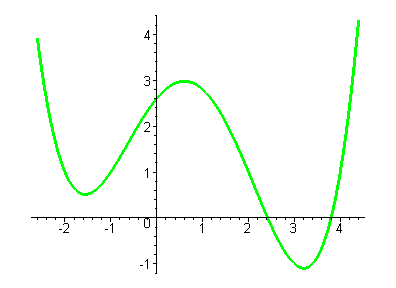
|
| Такого вида графики получаются, когда многочлен четвёртой степени имеет четыре различных действительных корня, |
|
| или когда два разных корня, а третий корень кратности два, |
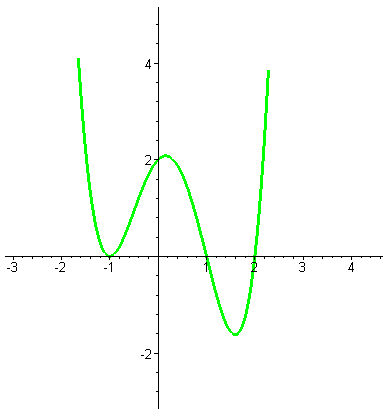
|
| или два корня кратности два. |
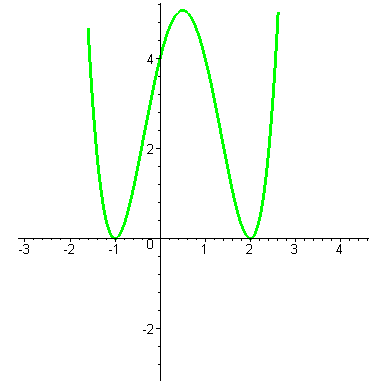
|
Пример 5.4.
Построить график функции 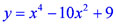 .
.
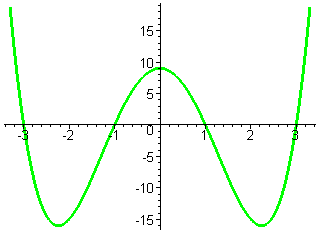
| Решение. Найдём корни многочлена, решив биквадратное уравнение, или более просто разложим многочлен на множители: 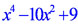 = = 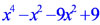 = = 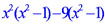 = == 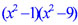 Многочлен имеет четыре различных корня: x1 = -3 , x2 = -1 , x3 = 1 , x4 = 3 . Отметим корни на оси абсцисс. |
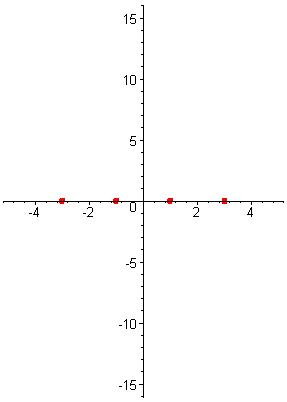
| |
| Построим график, учитывая, что данная функция, очевидно, чётная. f(-x) = 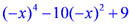 = = 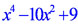 =
f(x) Функция сомметрична относительно оси OY . =
f(x) Функция сомметрична относительно оси OY .
|
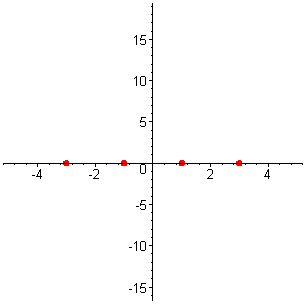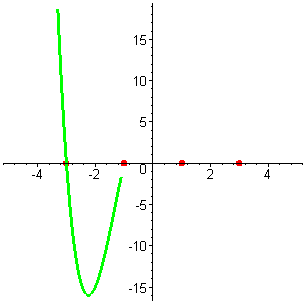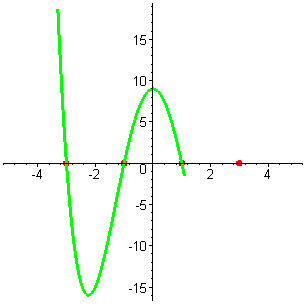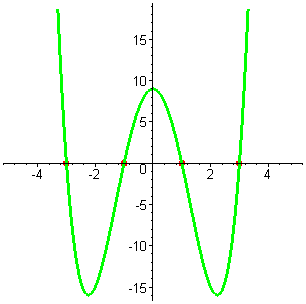
|
2 случай.
Производная многочлена четвёртой степени 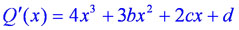 имеет два корня,
один из которых имеет кратность два, и значит, в этой точке экстремума нет. График в этом случае выглядит так:
имеет два корня,
один из которых имеет кратность два, и значит, в этой точке экстремума нет. График в этом случае выглядит так:
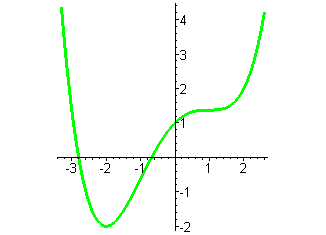
| Такого вида случай получается, если многочлен четвёртой степени имеет один простой корень, а другой кратности три. |
|
Пример 5.5.
Построить график функции 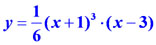 .
.
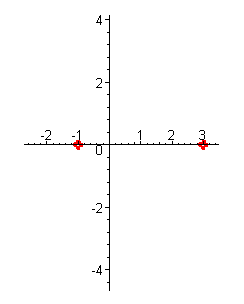
| Решение. Отметим корни многочлена на оси абсцисс: x1 = -1 , x2 = 3 . |
| |
Первый корень имеет кратность три, а значит, функция, переходя через корень,
будет менять свой знак, касаясь оси OX (смотри параграф 1 "Графики элементарных функций " график функции
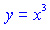 ). График будет выглядеть так: ). График будет выглядеть так:
|
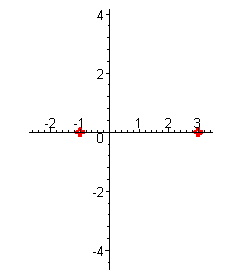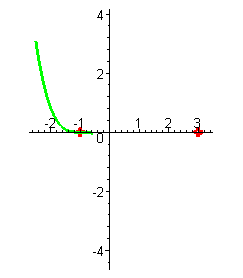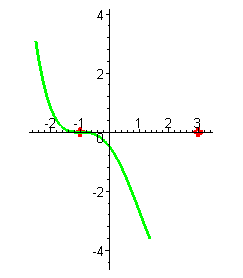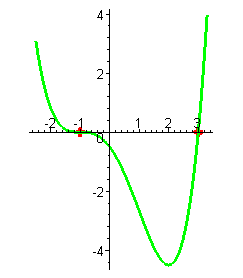
|
3 случай.
Производная многочлена четвёртой степени 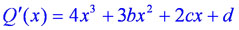 имеет один действительный корень.
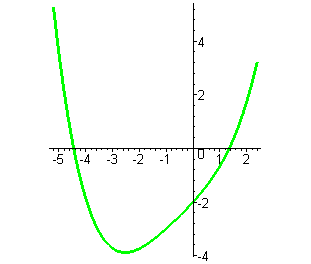
В этом случае многочлен имеет одну точку минимума и его график схож с графиком функции y=x4.
имеет один действительный корень.
В этом случае многочлен имеет одну точку минимума и его график схож с графиком функции y=x4.
Например, эта парабола четвёртой степени является графиком функции 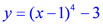
|
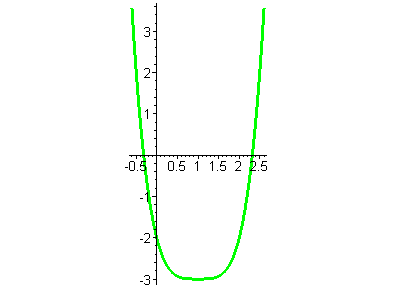
|
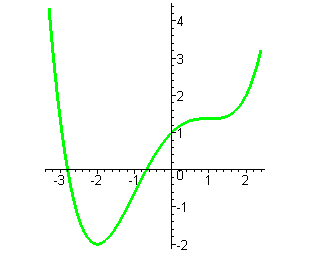
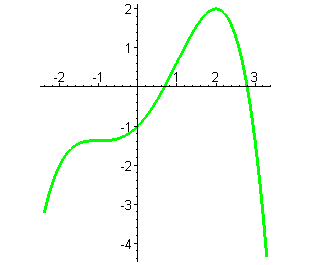
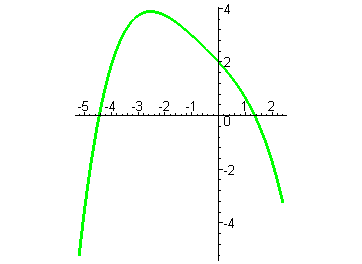
Аналогично строятся графики многочленов четвёртой степени с отрицательным старшим коэффициентом. В этом случае ветви параболы четвёртой степени направлены вниз. Получаем следующую сводную таблицу.
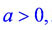 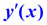 имеет 3 корня имеет 3 корня
|
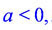 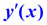 имеет 3 корня имеет 3 корня
|
|
|
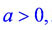 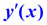 имеет 2 корня имеет 2 корня
|
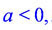 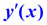 имеет 2 корня имеет 2 корня
|
|
|
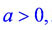 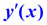 имеет 1 корень имеет 1 корень
|
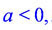 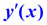 имеет 1 корень имеет 1 корень
|
|
|