Графики многочленов

Заметим, что под построением графика функции мы будем понимать построение схемы графика, то есть отражение характерных особенностей поведения функции, качественных характеристик: поведение функции на , наличие экстремумов, интервалы знакопостоянства, наличие вертикальных асимптот и поведение вблизи точек разрыва. Точное определение точек экстремумов возможно с помощью производной, однако это выходит за рамки нашего рассмотрения.

Построение графиков многочленов основано на двух свойствах.

Свойство 1.

Многочлен   P_n=a_n xⁿ+a_n-1 x^n-1+...+a₁ x+a₀  произвольной степени 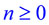    является непрерывной функцией, определённой для всех значений переменной. При больших положительных значениях переменной x многочлен принимает большие значения, совпадающие по знаку с коэффициентом a_n. При больших отрицательных значениях аргумента значения функции принимают большие значения, совпадающие по знаку с числом (-1)ⁿa_n .

Свойство 2. (Правило кратностей)

При прохождении многочлена через корень нечётной кратности его значения меняют свой знак на противоположный, а при прохождении через корни чётной кратности значения многочлена не меняют знака. Кратностью корня называется количество одинаковых сомножителей, отвечающих данному корню, в разложении многочлена на множители, т.е. показатель степени в разложении многочлена на множители.

Пример 5.1.

Многочлен 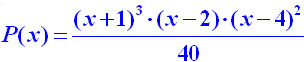имеет корень x1=-1 кратности три, корень x2=2 кратности один и корень x3=4 кратности два.
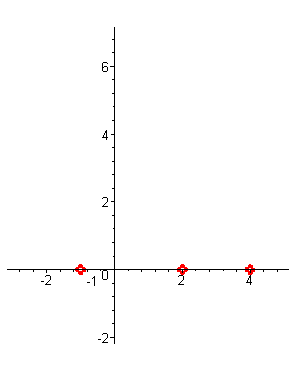
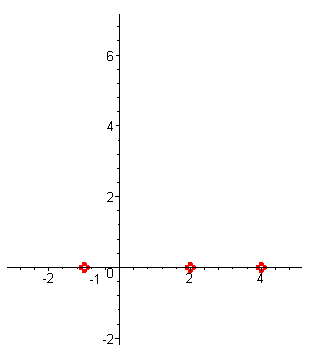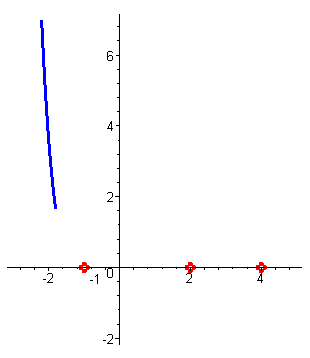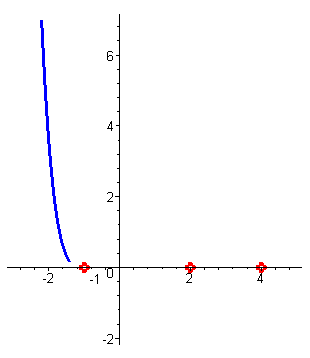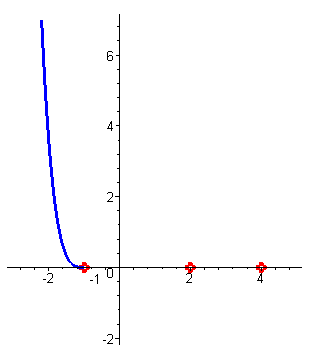
Построим схему графика этой функции. При больших отрицательных значениях аргумента (например, x=-100 ) значения функции – большие положительные числа. При приближении к первому корню x1=-1 значения функции уменьшаются, так как функция непрерывна, и при x1=-1 функция обращается в нуль. (Поведение ф-ции на участке от минус бесконечности до -1 - синий цвет)
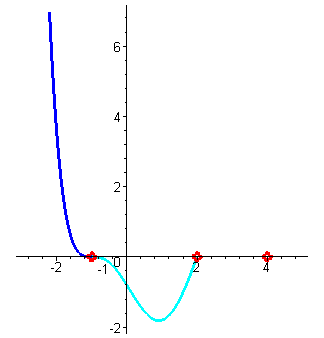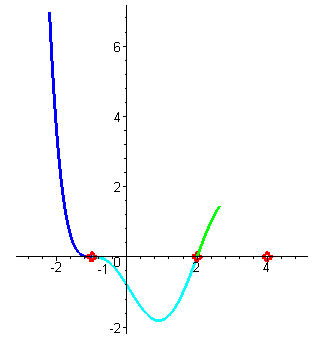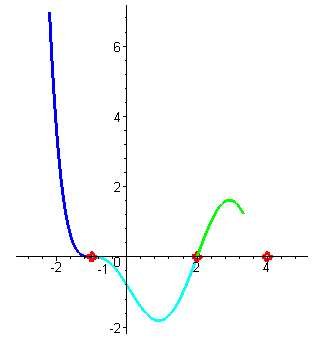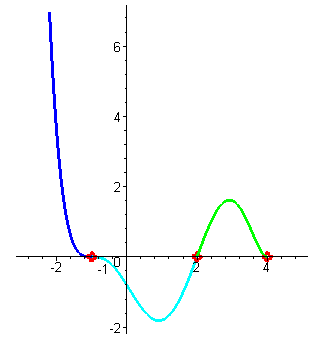
При переходе через корень значения функции меняют знак (кратность корня равна трём), а потом значения достигают снова нуля в корне x2=2 (поведение ф-ции на участке от -1 до 2 - голубой цвет) ,
снова меняют знак при переходе через корень, достигают некоторого максимального значения, потом уменьшаются до нуля в точке x3=4 . (Поведение ф-ции на участке от 2 до 4 - зеленый цвет)
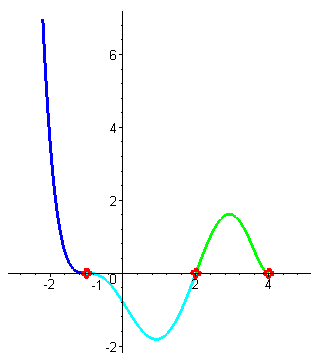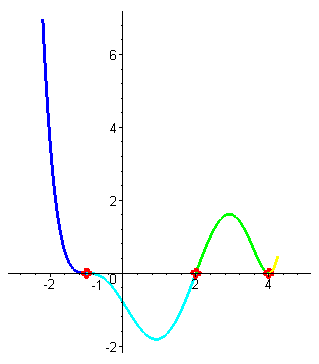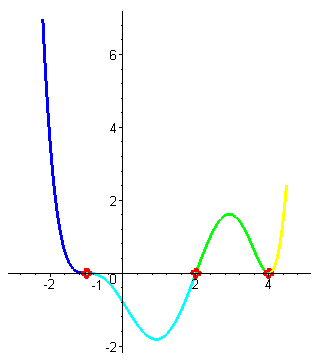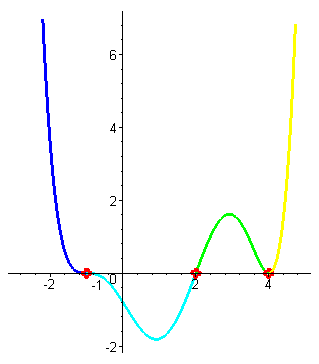
При переходе через этот корень значения функции не меняют знака (кратность корня равна двум, т.е. чётна). При увеличении значений аргумента значения функции неограниченно увеличиваются. (Пведение ф-ции на участке от 4 до плюс бесконечности - желтый цвет)
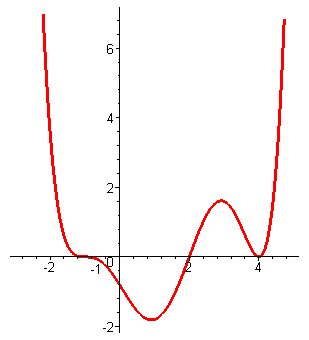
Итоговый график будет выглядеть следующим образом.

страницы: 1 2 3