Применяя вышеизложенные свойства многочленов, рассмотрим возможные схемы графиков многочленов третьей степени 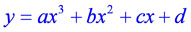. Пусть старший коэффициент многочлена a - положительное число.

1 случай.

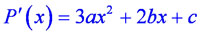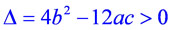Многочлен имеет две точки экстремума, в этом случае его производная имеет два различных корня, т.е. дискриминант этого квадратного трехчлена . Эта ситуация отражается в частных случаях, когда многочлен имеет три различных действительных корня x₁ , x₂ , x₃ , а также когда многочлен имеет два различных корня, один из которых имеет кратность два. В этом случае график имеет вид:

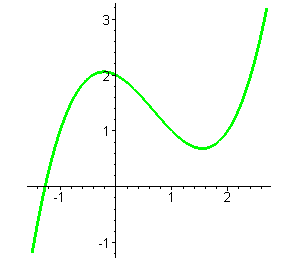
многочлен имеет 1 корень, а его производная - 2 корня
многочлен имеет 3 корня, а его производная - 2 корня
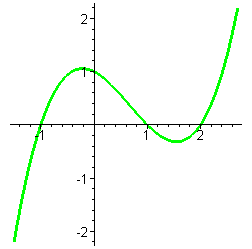
многочлен имеет 2 корня и его производная - 2 корня

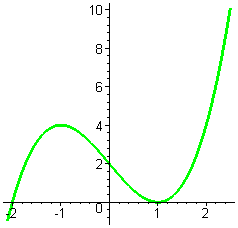
2 случай.

У многочлена нет экстремумов, т.е. .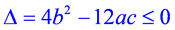

В этом случае график представляет собой монотонно возрастающую функцию.

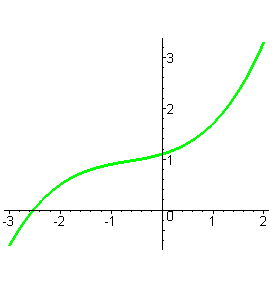
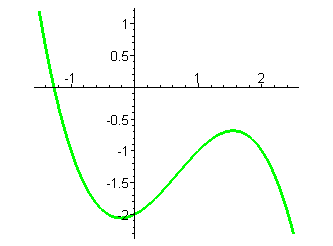
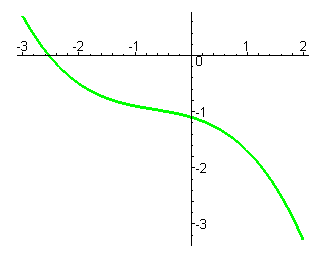
Аналогично строятся графики кубических парабол при отрицательном старшем коэффициенте. Получаем сводную таблицу различных видов графиков многочленов третьей степени: .

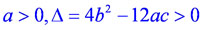
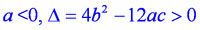
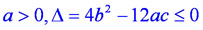
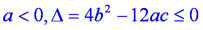
Пример 5.2.
Построить график функции .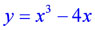

Решение. Разложим многочлен на множители: 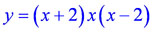. Отметим на оси абсцисс корни функции: -2;0;2 .
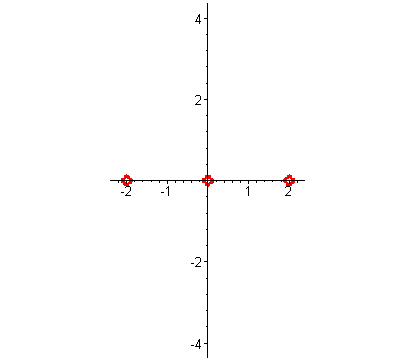
При больших отрицательных значениях x значения функции – большие отрицательные числа. Применяя свойство непрерывности и свойство кратностей ( все корни кратности один - в точке пересечения функция меняет знак на противоположный ) , замечая, что при неограниченном возрастании x значения функции стремятся к плюс бесконечности, строим схему графика функции.

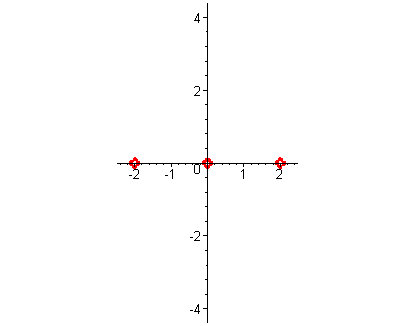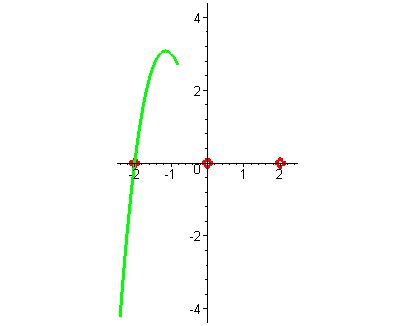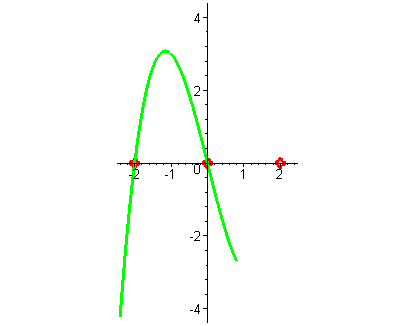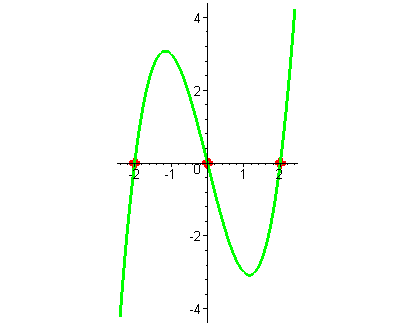
Пример 5.3.
Построить график функции .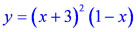

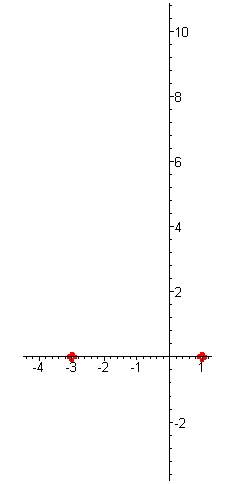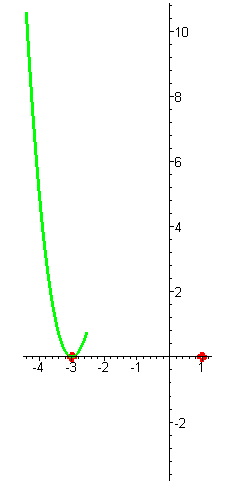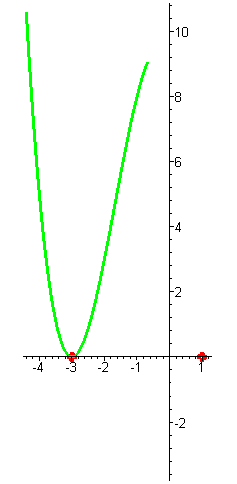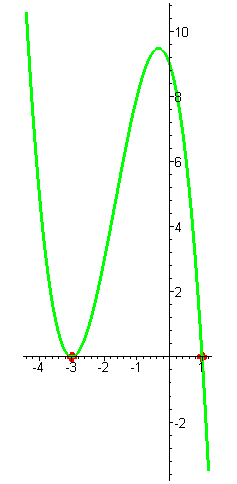
Решение. Многочлен имеет два корня: x1 = -3 кратности два и x2 = 1 кратности один.

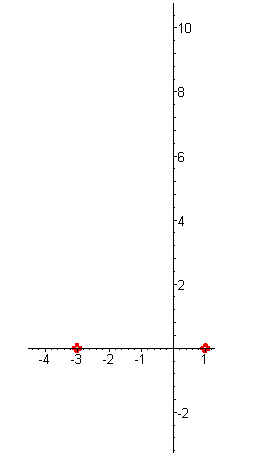
При больших отрицательных функция принимает большие положительные значения. При приближении аргумента к числу -3 значения функции убывают и стремятся к нулю. При переходе через корень значения функции не меняют знак (кратность корня чётна), на интервале (-3;1) функция достигает максимума, так как при x = -3 она снова обращается в нуль. При переходе через корень x =1 функция меняет свой знак с положительного на отрицательный (кратность корня нечётна) и стремится к минус бесконечности при неограниченном увеличении аргумента.

страницы:1 2 3