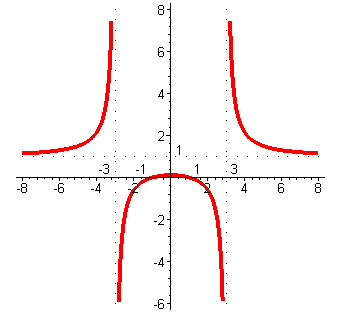
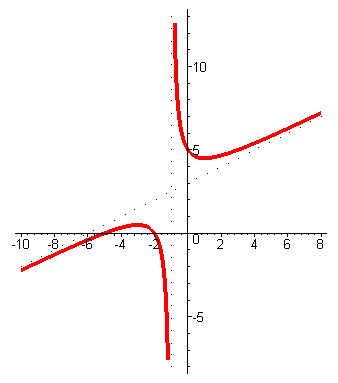
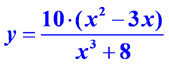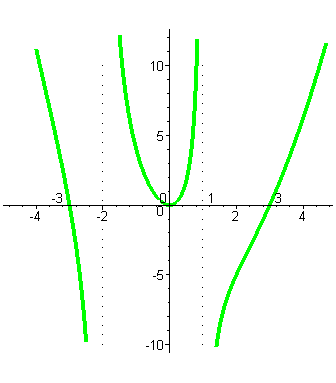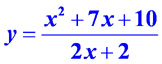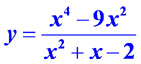Графики дробно-линейной и дробно-рациональной функций

Дробно-рациональной функцией называется отношение двух многочленов:     , коэффициенты при степенях x -действительные числа, причём, будем предполагать, что числитель и знаменатель дроби не имеют общих линейных сомножителей. При построении графика дробно-рациональной функции надо исследовать поведение функции на бесконечности, а также вблизи нулей знаменателя, которые определяют вертикальные асимптоты графика.

Рассмотрим поведение функции на . Возможны 4 случая.

1) n<m . Если степень числителя меньше степени знаменателя, то дробно-рациональная функция стремится к нулю при стремлении x  к .

2) n=m . В этом случае предел функции на равен отношению старших коэффициентов, это значит, что у функции будет горизонтальная асимптота     .

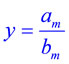3) n=m+1 . В этом случае у функции будет наклонная асимптота y=kx+b , которая получается в результате деления числителя дроби на знаменатель:     .

4) n≥m+2 . Значения функции стремятся к при стремлении аргумента x к . Знак бесконечности легко определяется по степеням старших членов n,m и коэффициентам a_n ,b_m при старших степенях, а именно, на + ∞ знак определяется знаком произведения a_n·b_m , а на - ∞ - знаком выражения (-1)^n-m·a_n·b_m .

Теперь рассмотрим поведение дробно-рациональной функции вблизи точек разрыва, т.е. нулей знаменателя. Пусть 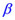- корень знаменателя кратности k . Это значит, что при разложении знаменателя на множители одним из сомножителей будет двучлен 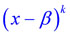. При приближении аргумента x к 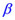числитель дроби представляет некую константу, отличную от нуля, а знаменатель стремится к нулю, а значит, дробь будет неограниченно возрастать по абсолютной величине, стремясь к . Таким образом, прямая будет вертикальной асимптотой графика функции. Знак бесконечности, к которой стремится функция слева и справа от , можно определить непосредственно подстановкой вместо x в выражение функции числа, близкого к числу 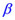с недостатком (слева) или с избытком (справа), но обычно этот знак определяется по методу интервалов, если нам известны корни числителя и знаменателя.

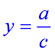Рассмотрим частный случай дробно-рациональной функции: дробно-линейную функцию  , в числителе и знаменателе которой линейные функции. Графиком дробно-линейной функции является гипербола. Расположение гиперболы определяется вертикальной асимптотой и горизонтальной асимптотой. Вертикальная асимптота - это нуль знаменателя, то есть прямая , а горизонтальная асимптота-прямая ( случай 2 : n=m). Заметим, что рассматривая дробно-линейную функцию, мы предполагаем, что с ≠ 0 , иначе функция будет линейной, и её графиком будет прямая линия.

Графики дробно-линейной функции

Рассмотрим примеры.

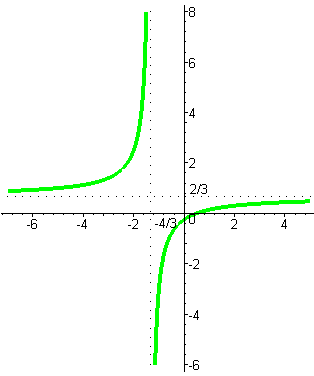Построить график функции	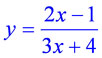Построить график функции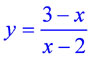