Задание:

Постройте график функции

Решение:

Разложим числитель и знаменатель на множители:.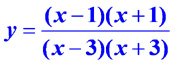
Найдём корни числителя и знаменателя. Эта функция определена при всех x ≠ -3;3 (нули знаменателя). В точках x=1 и x= -1 функция равна 0.

Отметим на числовых осях корни числителя и знаменателя. Исследуем поведение функции в окрестности точек x= -3 и x=3. Убедимся, что вертикальные прямые x= -3 и x=3 будут вертикальными асимптотами графика функции. Когда аргументx приближается к числу 3 справа, например, принимает значения: 3,1; 3,01; 3,001; и т.д., то соответствующие значения функции возрастают и стремятся к + ∞ , так как числитель дроби близок к числу 8, а знаменатель становится все меньше, приближаясь к нулю, оставаясь положительным, а значит дробь неограниченно возрастает, а это и означает, что график функции приближается к вертикальной прямой x=3 справа, неограниченно возрастая ( зеленый цвет).
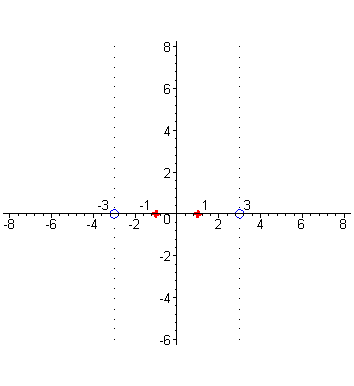
Когда аргумент x приближается к числу 3 слева, например принимает значения 2,9; 2,99; 2,999; …, то то соответствующие значения функции принимают все большие по абсолютной величине отрицательные значения, так как числитель по прежнему близок к числу 8, а знаменатель становится все меньше, приближаясь к нулю, а значит дробь становится все большим по абсолютной величине отрицательным числом, т.е. стремится к - ∞ , но это означает, что график функции приближается слева к вертикальной прямой x = 3 неограниченно убывая ( цвет морской волны).
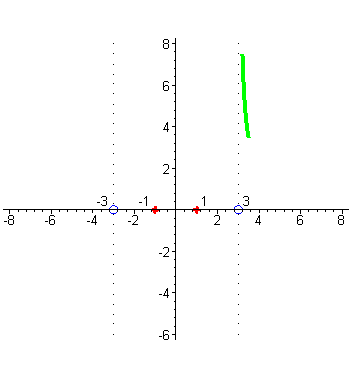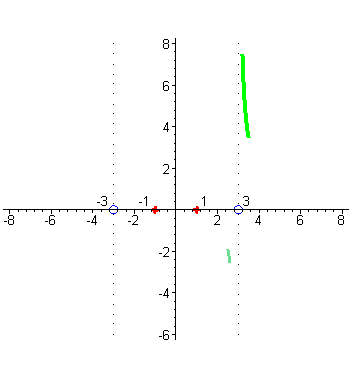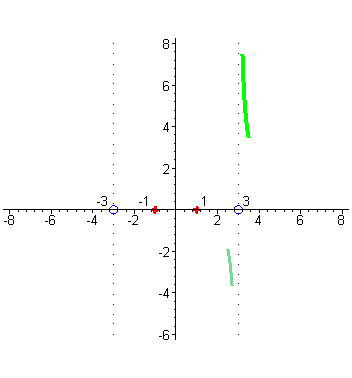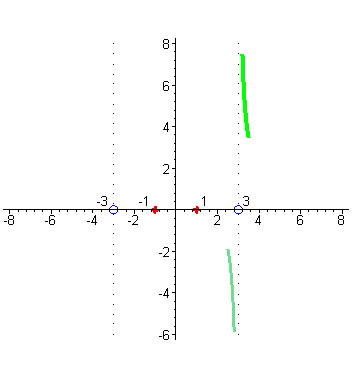
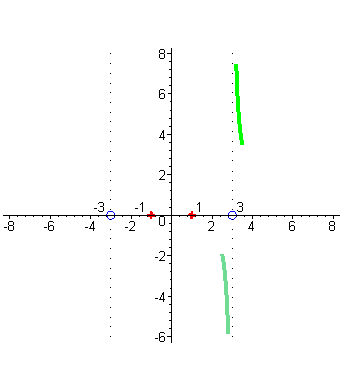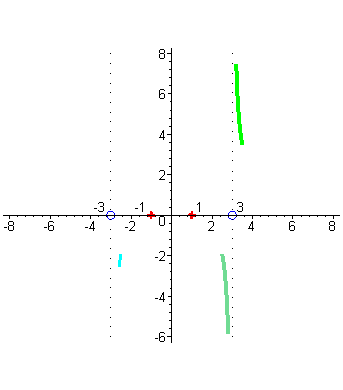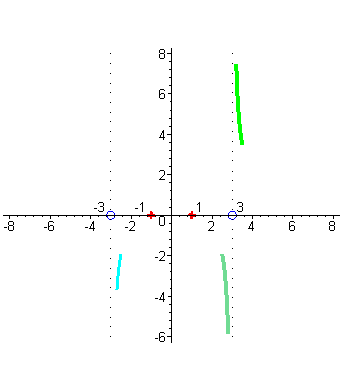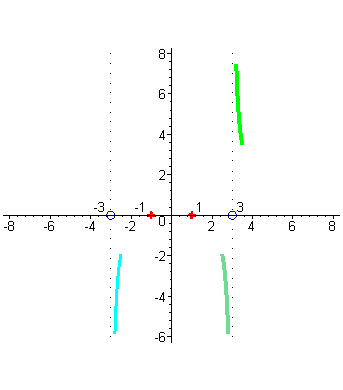
Аналогично разбирается случай поведения графика вблизи точки x= -3. В окрестности точки -3 числитель близок к числу 8, а знаменатель стремится к нулю при приближении аргумента x к числу -3, но для точек близких к -3 справа знаменатель представляет собой близкое к нулю отрицательное число ( голубой цвет),
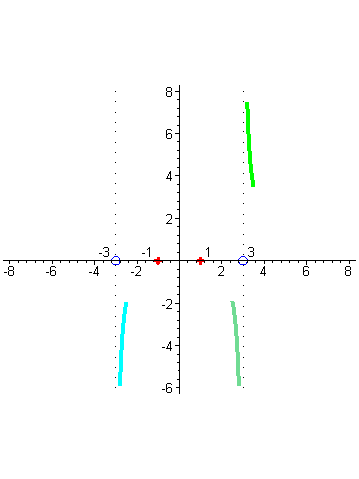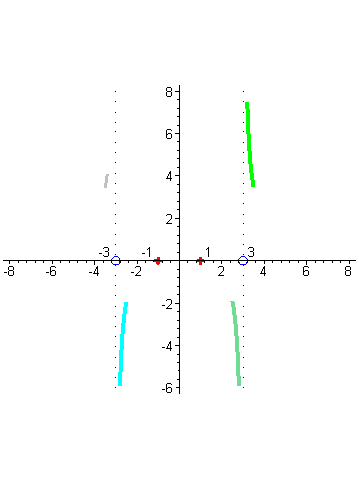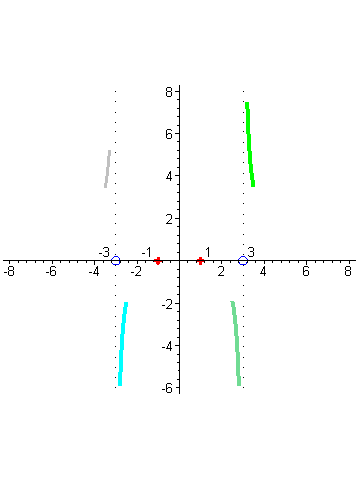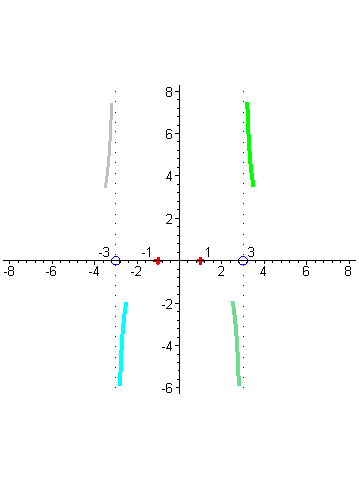
а слева – близкое к нулю положительное число (серый цвет). Это значит, что слева от -3 график дроби неограниченно возрастает, приближаясь прямой x= -3, а справа неограниченно убывает.
Рассмотрим поведение функции на ± ∞ , т.е. как ведет себя график при больших отрицательных и больших положительных значениях переменной x (желтый цвет). Легко понять, что при больших по абсолютной величине x значения числителя близки к числу x2 так же, как и значения знаменателя. Так, при x = 1000000 x2-1 = 10000002-1 ≈ 10000002 x2-9 = 10000002-9 ≈ 10000002 Причем, чем x больше, тем это приближение точнее. Значит дробь 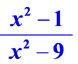при больших x как положительных, так и отрицательных близка к 1, то есть, график функции справа и слева стремится к горизонтальной прямой y = 1, причем сверху, так как для больших положительных и отрицательных x числитель немного больше знаменателя.
Завершаем построение графика пользуясь непрерывностью нашей функции на промежутках ( -∞; 3 ); ( -3; 3) и ( 3; +∞) . Вспоминаем, что в точках x= ±1 функция обращается в ноль, а при переходе через эти точки меняет свой знак, так как оба корня кратности один, т.е. простые.
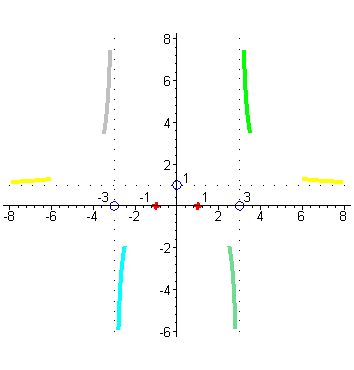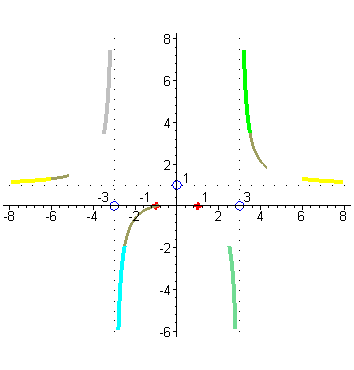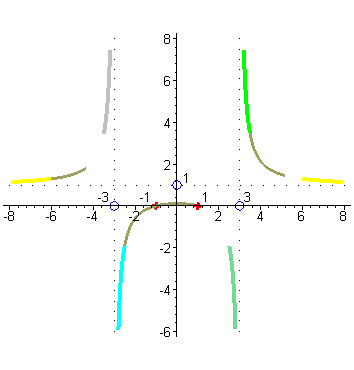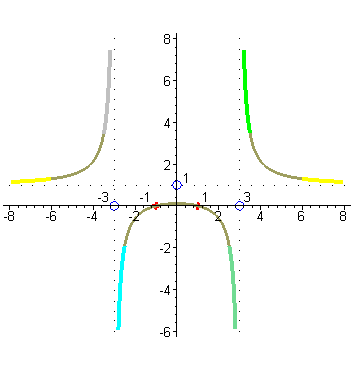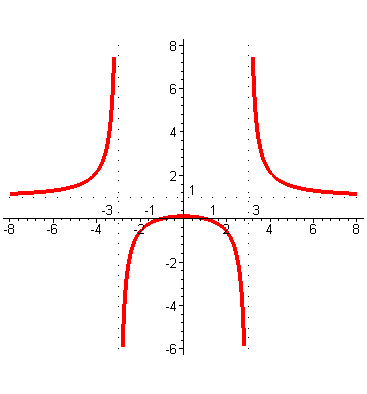
Кончный график будет выглядеть так.