Задание:

Постройте график функции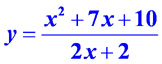

Решение:

Заметим, что степень числителя на единицу больше степени знаменателя ( n=m+1), поэтому у графика функции имеется наклонная асимптота.

Для её нахождения разделим числитель на знаменатель, получим: 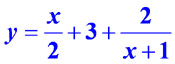. Из этой записи видно, что при больших x, как положительных, так и отрицательных, дробь 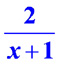является маленьким числом , а значит, значения функции близки к значениям прямой 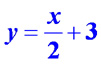, которая и является наклонной асимптотой.
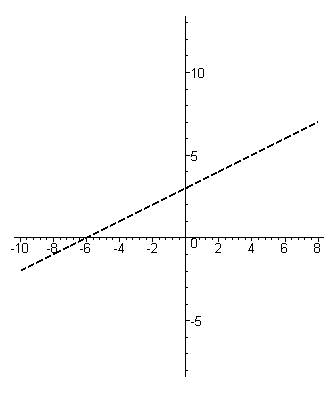
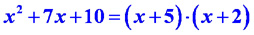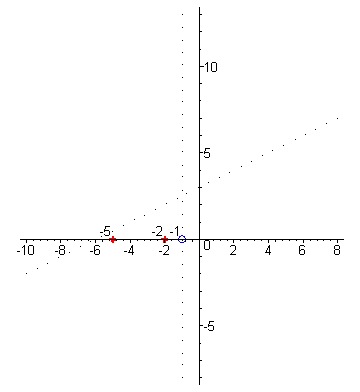
Найдём корни числителя, для этого разложим числитель на множители: . Отметим на числовой оси OX корни числителя x=-5; x=-2 и корень знаменателя x=-1, который даёт вертикальную асимптоту.
Начнём построение графика справа от асимптоты : при аргументах близких к x=-1 справа (например, x=-0,99) значения функции –большие положительные числа , так как знаменатель - маленькое положительное число, а числитель близок к 4.
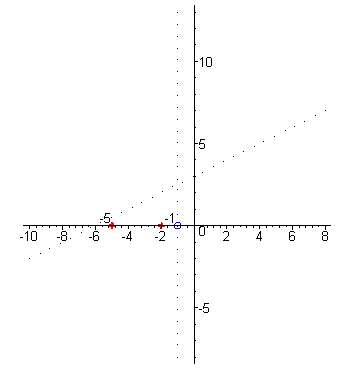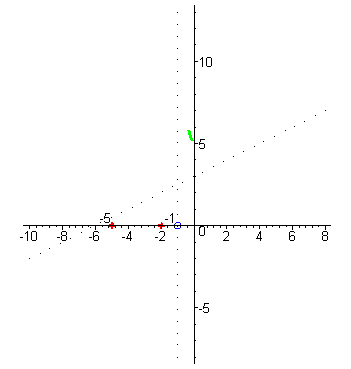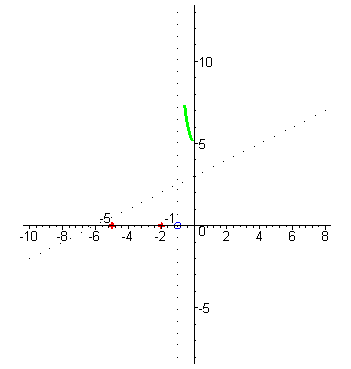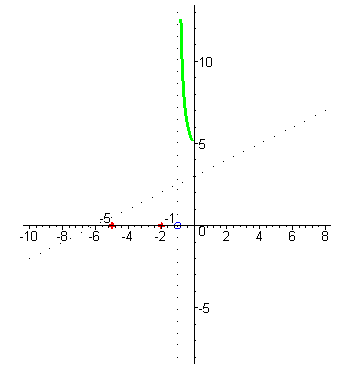
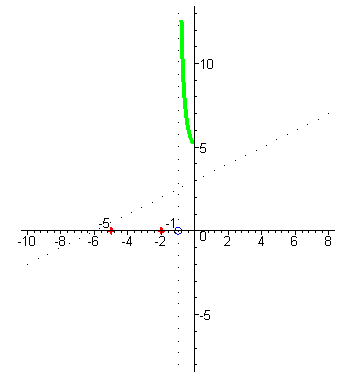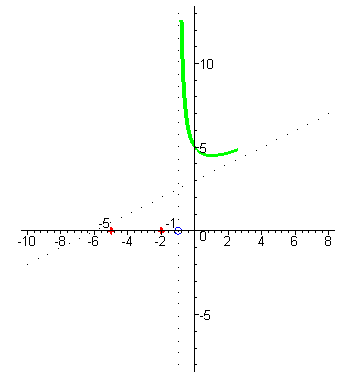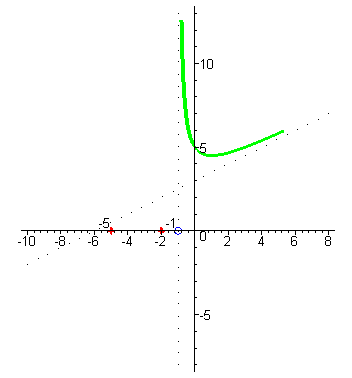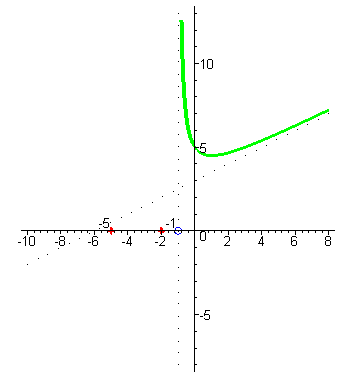
При увеличении значений x значения функции сначала уменьшаются до минимума, а потом начинают увеличиваться и стремятся к наклонной асимптоте.
При аргументах x близких к -1 слева (например, x= -1,01) значения функции – большие отрицательные числа, это ещё проще усмотреть на основании метода интервалов: корень знаменателя имеет кратность один, а значит при переходе через -1 знак функции меняется.
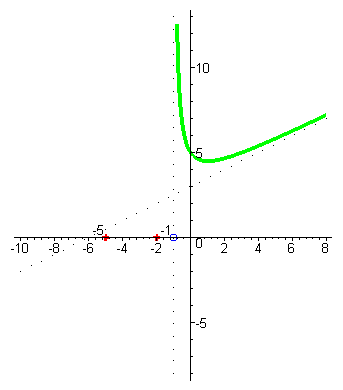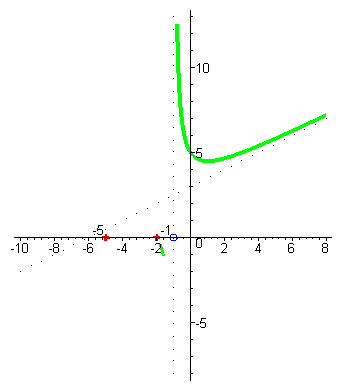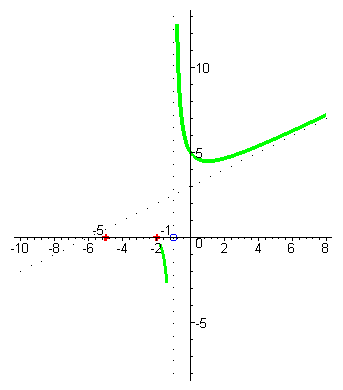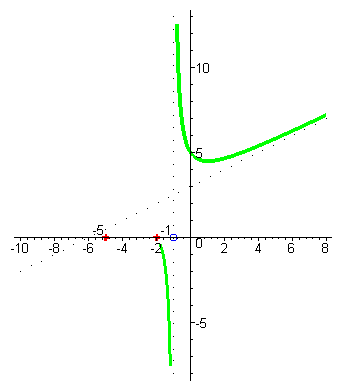При уменьшении значений x и подходе к корню числителя x= -2 значения функции стремятся к нулю, при переходе через -2 функция меняет знак с отрицательного на положительный, затем приходит в корень x= -5, снова меняет знак, и при дальнейшем уменьшении аргумента стремится к наклонной асимптоте.
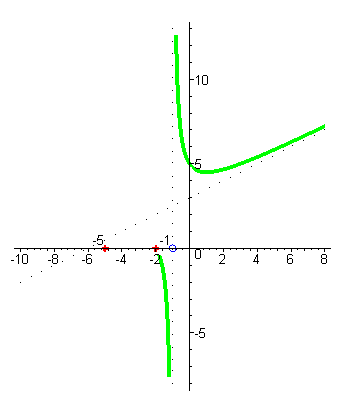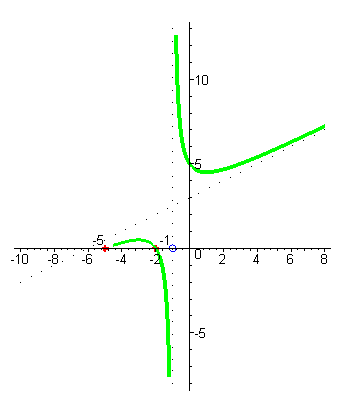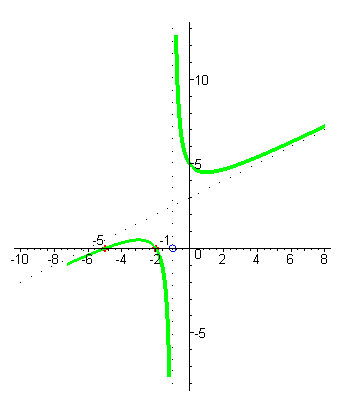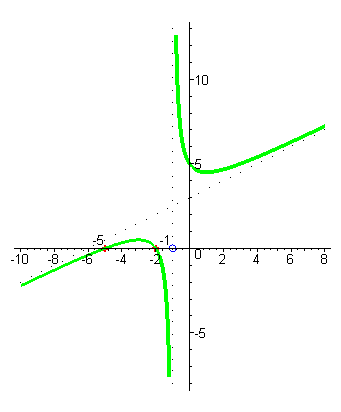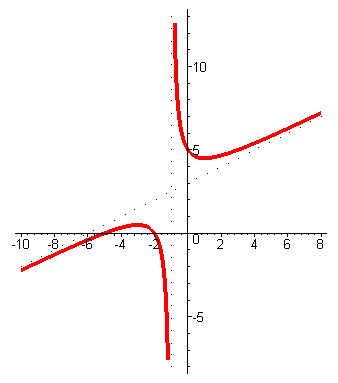
Кончный график будет выглядеть так.