Методы графического сложения, вычитания

Чтобы построить график функции y = f(x) + g(x) , надо построить на одном чертеже графики y = f(x) и y = g(x) , потом при каждом x сложить ординаты двух графиков.

Если необходимо построить график разности двух функций y = f(x) - g(x) , то этот случай сводится к построению суммы: y = f(x) + ( - g(x)) . Причем, график функции y = - g(x) получается из графика функции y = g(x) симметричным отражением относительно оси OX .

В случае, когда вторая функция - константа, то графическое сложение означает сдвиг графика первой функции по вертикали на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.

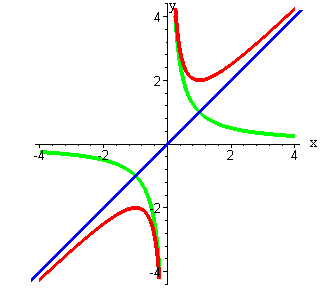
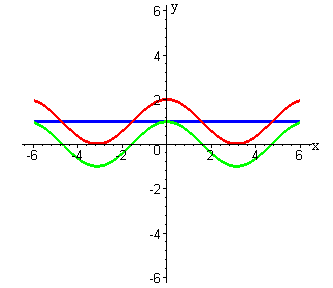
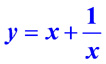
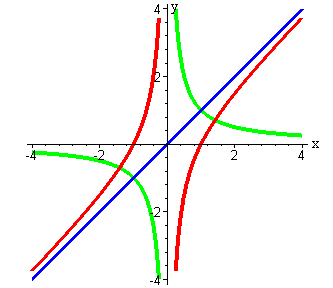
Сложение двух функций:	Вычитание двух функций: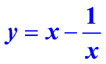
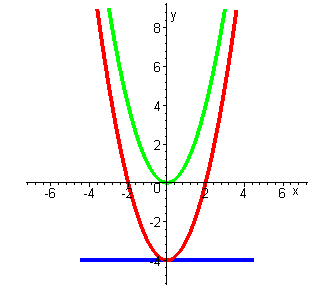
Сложение функции и константы:	Вычитание функции и константы: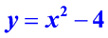

Методы графического умножения, деления

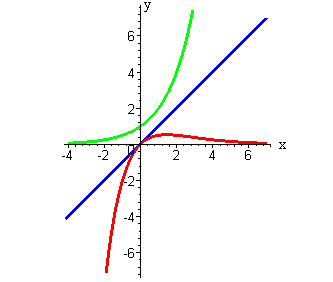
Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и y=g(x) , потом при каждом x перемножить ординаты двух графиков.

Графическое деление выполняется аналогично произведению.

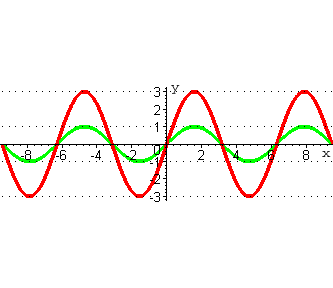
В частном случае при построении графика функции y=A·f(x) , где A - константа надо график функции y=f(x) растянуть в |A| раз по вертикали, при условии |A|≥1 , или сжать в раз по вертикали, если |A|<1 , и затем полученный график отобразить симметрично относительно оси OX, если A<0 .

В данном параграфе рассмотрены следующие примеры:

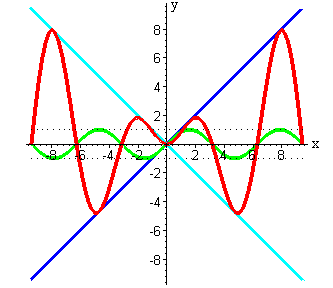
Умножение двух функций: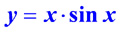	Делениее двух функций: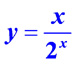

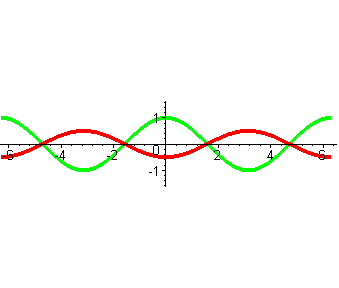
Умножение функции на константу A > 0: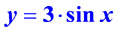	Умножение функции на константу A < 0: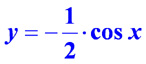