Общие принципы построения графиков
При построении графиков функций невозможно обойтись без общих подходов, таких как общие свойства функций: четность, нечетность, периодичность, - а также исследование поведения функции на бесконечности и вблизи точек несуществования функции. Причем, исследование функции в окрестности этих точек и на бесконечности имеет, как правило, арифметический характер.
Напомним определение основных свойств функции.
Определение.
Функция y=f(x) называется четной, если
1) область определения этой функции симметрична относительно нуля на числовой прямой, т.е. для любого
x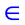 Df (область определения функции) -x
Df (область определения функции) -x
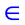 Df
Df
2) для любого x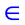 Df f(-x)= f(x).
Df f(-x)= f(x).
Из определения следует, что график четной функции симметричен относительно оси OY.
Примеры четных функций: y=x2, y=cos(x).
Определение.
Функция y=f(x) называется нечетной, если
1) область определения этой функции симметрична относительно нуля на числовой прямой, т.е. для любого
x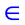 Df -x
Df -x
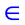 Df
Df
2) для любого x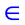 Df f(-x)=- f(x).
Df f(-x)=- f(x).
График нечетной функции симметричен относительно начала координат.
Примеры нечетных функций: y=x3, y=sin(x).
Заметим, что сами понятия: четная, нечетная функции первоначально связаны со свойствами степенной функцииy=xn . При четном n степенная функция четная, а при нечетном n – нечетная.
Определение.
Функция y=f(x) называется периодической,
если существует такое положительное
число T, что
1) для любого x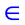 Df
(x+T)
Df
(x+T)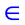 Df,
(x-T)
Df,
(x-T)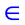 Df
Df
2) для любого x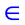 Df f(x+T)= f(x-T)= f(x).
Df f(x+T)= f(x-T)= f(x).
Наименьшее из всех таких чисел T называется основным периодом функции y=f(x).
Примеры четных функций: y=sin(x) период T= 2π, y=tg(x) период T=π.
При построении графиков используется следующая теорема.
Теорема.
Если y=f(x) периодическая функция с периодом T, то функция y=f(kx+b) - периодическая
с периодом 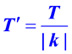 , при k≠0.
, при k≠0.
Из определения периодической функции следует, что построения ее графика достаточно выполнить на любом отрезке длинны
T,
например[ 0, T ] или 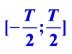 , где T – период функции, а в остальных точках значения функции «повторяются».
Это существенно упрощает исследование, нахождение точек экстремума, точек разрыва, и поведение функции вблизи этих точек.
Например, построение графика функции y=sin2x-sinx достаточно выполнить на отрезке
[0,2π], так как
T=2π, очевидно, является
периодом этой функции. А при построении графика y=cos2x+cosx
достаточно ограничиться отрезком [0,π], так как кроме периодичности
с периодом T=2π функция обладает свойством четности, что в два раза сокращает отрезок исследования.
, где T – период функции, а в остальных точках значения функции «повторяются».
Это существенно упрощает исследование, нахождение точек экстремума, точек разрыва, и поведение функции вблизи этих точек.
Например, построение графика функции y=sin2x-sinx достаточно выполнить на отрезке
[0,2π], так как
T=2π, очевидно, является
периодом этой функции. А при построении графика y=cos2x+cosx
достаточно ограничиться отрезком [0,π], так как кроме периодичности
с периодом T=2π функция обладает свойством четности, что в два раза сокращает отрезок исследования.
При построении графиков элементарных функций используется еще один основополагающий принцип, который явно не упоминают: элементарная функция непрерывна всюду в области определения.
При построении графиков дробно-рациональных функций, т.е. функций вида 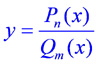 , где
, где 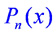 и
и 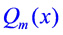 - многочлены степеней n и m
соответственно, большую роль играет поведение функции на
- многочлены степеней n и m
соответственно, большую роль играет поведение функции на  и в окрестности точек обращающих знаменатель дроби в нуль.
и в окрестности точек обращающих знаменатель дроби в нуль.
Подробнее эту ситуацию рассмотрим в теме "Графики дробно-линейной и дробно-рациональной функций".