Итак, мы видим какую роль играет умение построить графики для решения алгебраических задач. Напомним, как выглядят графики основных элементарных функций.

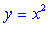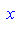График функции представляет собой параболу (кривую, состоящую из двух бесконечных ветвей, симметричных относительно оси ординат). может принимать любые значения, множество значений функции все неотрицательные действительные числа.
График функци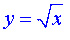и лежит в I координатной четверти. Из предыдущего графика зависимости ( 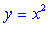) мы видим, что корень из отрицательного числа не существует. Поэтому область определения функции от 0 до + ∞.
График функции 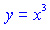лежит в I и III координатной четверти, поскольку отрицательным значениям 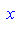соответствуют отрицательные значения .
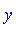Аналогично предыдущему графику график функции 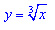лежит в I и III координатной четверти.
Функция 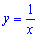задает обратнопропорциональную зависимость. Ее график - гипербола состоит из двух отдельных частей, каждая из которых имеет две бесконечные ветви. Одна из которых приближается к оси абсцисс, другая - к оси ординат. Областью определения этой функции является совокупность всех действительных чисел, за исключением нуля.

страницы: 1 2 3