| Графики элементарных функций |
Показательная функция ![]() (
( ![]() > 0 )
определена при всех значениях
> 0 )
определена при всех значениях ![]() от -
от - ![]() до +
до + ![]() .
При всех значениях
.
При всех значениях ![]() функция больше нуля.
функция больше нуля.
| Если |
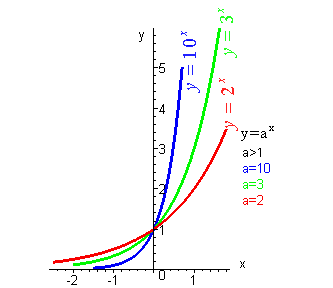
|
| Если 0 < Заметим, что при a = 1 ax ≡ 1. → График функции - прямая линия параллельная оси абсцисс. |
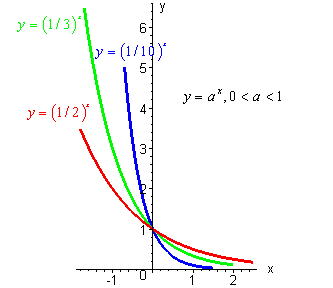
|
Функция ![]() называется логарифмической.
Показательная функция при основании
называется логарифмической.
Показательная функция при основании ![]() и логарифмическая функция при том же основании представляют пример
двух обратных друг другу функций. Графиком функции
и логарифмическая функция при том же основании представляют пример
двух обратных друг другу функций. Графиком функции
![]() будет служить кривая, получаемая из графика функции
будет служить кривая, получаемая из графика функции
![]() посредством преобразования симметрии относительно прямой
посредством преобразования симметрии относительно прямой
![]() . Область определения функции
. Область определения функции
![]() >0 ,так как отрицательные
числа и число 0 логарифмов не имеют. Логарифм единицы равен нулю.
>0 ,так как отрицательные
числа и число 0 логарифмов не имеют. Логарифм единицы равен нулю.
| При |
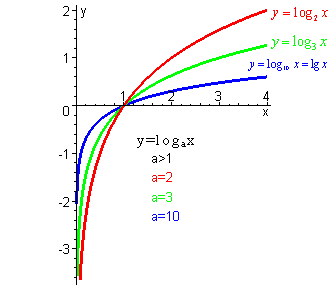
|
| При 0 < |

|