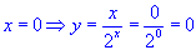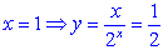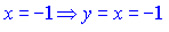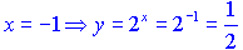Задание:

Постройте график функции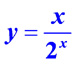    

Решение:

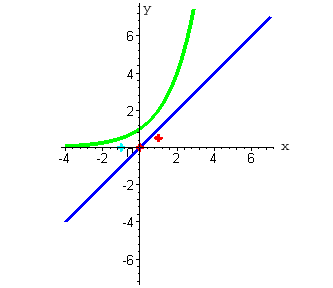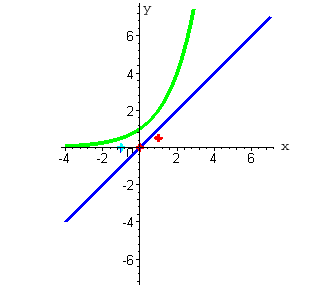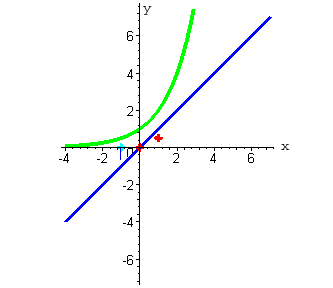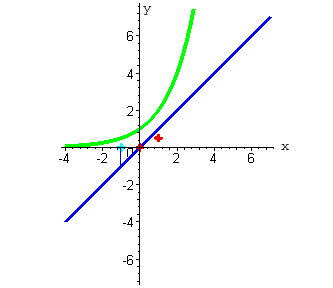
Построим на одном чертеже графики функций y=x и y=2x . Далее идем вдоль оси OX слева направо и при каждом фиксированном значении аргумента делим значение первой функции на соответствующее значение второй.
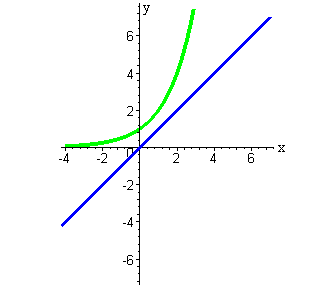
Рассмотрим подробно следующие точки: 1. При x =0 числитель функции частного равен 0 ( знаменатель не равен 0), значит график функции 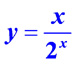проходит через начало координат. Отметим эту точку красным цветом.
2. При x =1 функция y=x принимает значение равное единице (ординаты синего цвета). Функция y=2x в этой точке принимает значение равное 2 ( при нажатии на кнопку "следующая" - ординаты зеленого цвета).
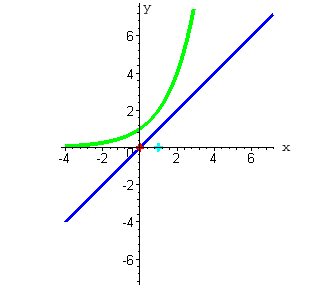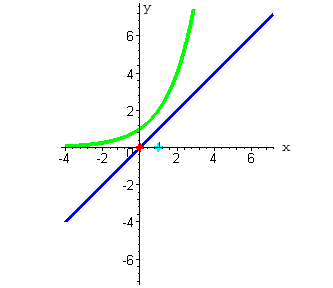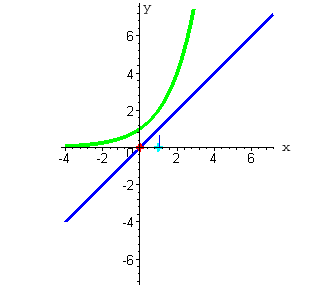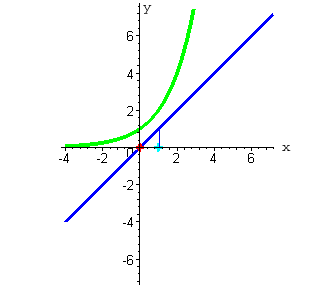
Функция 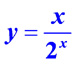  принимает значение равное 1/2 . Мы получили вторую точку, через которую проходит график искомой функции.
3. При x = -1 функция y=x принимает значение равное минус единице. Функция y=2x принимает значение равное 1/2 .
Функция 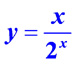  принимает значение равное -2 . Мы получили третью точку, через которую проходит график искомой функции.
Аналогично получаем другие точки. Теперь можно выявить закономерности поведения графика частного двух функций. Так, например, видно, что при больших отрицательных значениях аргумента значения частного двух функций - большие отрицательные числа. При стремлении аргумента к нулю значения функции тоже стремятся к нулю. Пересекая ось OX в нуле, функция будет возрастать пока не достигнет максимума, а потом будет убывать и стремиться к нулю.
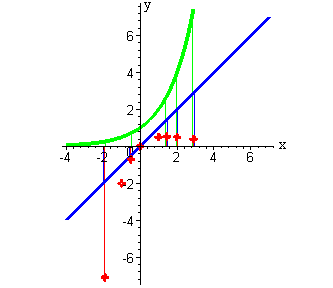
На представленном графике изображены делимое (синий цвет), делитель (зеленый цвет) и частное (красный цвет).
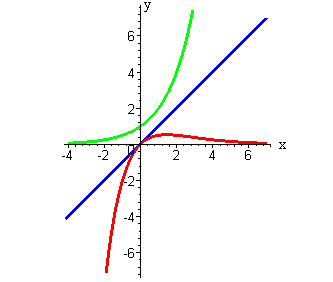