Задание:

Постройте график функции y=x·sin x

Решение:

Построим графики функций y=x и y=sin x.
Далее при каждом x перемножим ординаты двух графиков. Сначала рассмотрим точки, в которых функция y=sin x принимает нулевые значения. В этих точках значения функции произведения тоже будут равны 0 . Отметим эти точки красным цветом.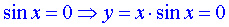
Теперь рассмотрим точки, в которых функция y=sin x принимает значения равные единице (они обозначены голубым цветом). В этих же точках определяем значения функции y=x ( при нажатии на кнопку "следующая" - ординаты синего цвета).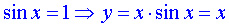
Значения функции произведения в этих точках будут равны значениям функции y=x.
Далее рассмотрим точки, в которых функция y=sin x принимает значения равные минус единице (они обозначены голубым цветом).В этих же точках определяем значения функции y=x ( при нажатии на кнопку "следующая" - ординаты синего цвета).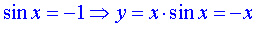
Значения функции произведения в этих точках будут противоположны по знаку и равны по абсолютной величине значениям функции y=x. Поэтому, чтобы получить значение функции произведения в этих точках, нужно отложить ординаты функции y=x в этих точках с противоположным знаком.
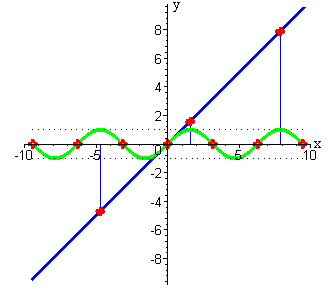
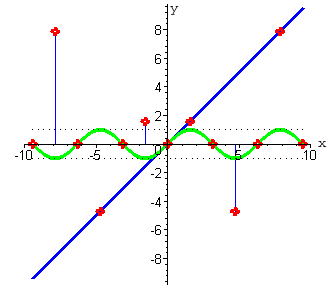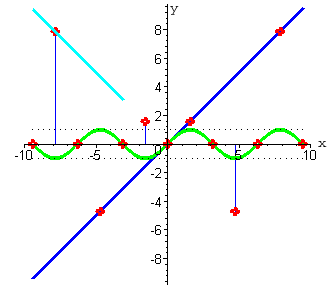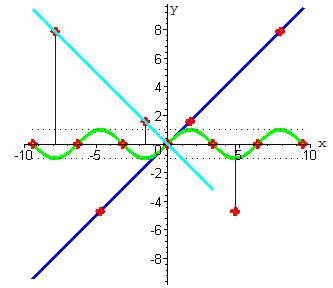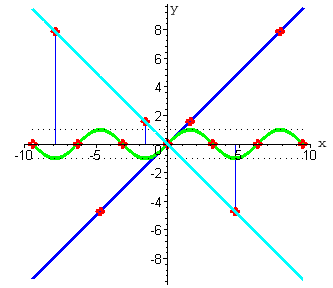
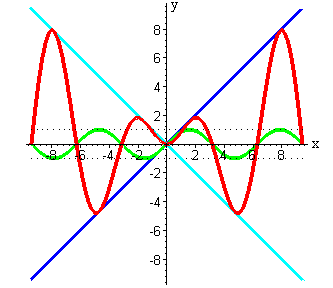
Итак, мы получили значения функции произведения в рассматриваемых точках. Мы видим, что эти значения принадлежат прямой y= -x . Для наглядности проведем ее голубым цветом.
Теперь мы знаем, что искомая кривая будет ограничена прямыми y=x и y= -x , эта кривая будет периодичной функцией (так как получается в результате умножения на периодичную функцию y=sin x ). Через полученные точки, соответствующие значениям функции произведения, проводим кривую красным цветом.
Заметим, что функция y=x·sin x четная, то есть её график симметричен относительнo оси OY. Поэтому построение графика можно было производить только при положительных аргументах, а затем симметрично отразить полученную кривую относительно оси OY.