Задание:
Постройте график функции 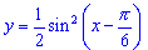
Решение:
Преобразуем данное выражение функции по формуле понижения четной степени синуса:

Представим это выражение в виде суммы :  .
.
Попробуем получить график, соответствующий данному выражению, путем элементарных преобразований графика y=cos x.
|
Построим график функции y=cos x. Сожмем этот график в два раза вдоль оси OX к оси OY. |

|
| Получим график функции y=cos 2x(обозначим его желтым цветом).
Мы видим, что наименьший положительный период уменьшился в 2 раза. Осуществим параллельный перенос предыдущего графика на  вправо вдоль оси абсцисс. вправо вдоль оси абсцисс. |

|
Так мы получим график функции  (изобразим его серым цветом).
Штрихпунктирная линия показывает, на сколько сместился график относительно оси OY. (изобразим его серым цветом).
Штрихпунктирная линия показывает, на сколько сместился график относительно оси OY.
|

|
| Сожмем третий график в четыре раза к оси абсцисс. Горизонтальные пунктирные линии наглядно показывают, как изменится при этом амплитуда изменения значений функции. |

|
Получим график функции  ( изобразим его голубым цветом). ( изобразим его голубым цветом).
|
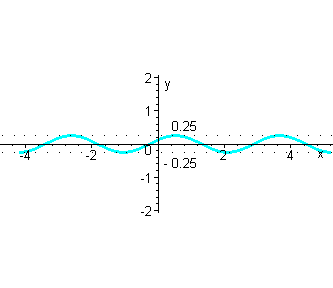
|
Построим график функции 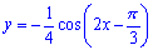 симметричным отражением относительно оси
абсцисс предыдущего графика.
Для того чтобы полученный график отобразить симметрично относительно оси OX, мы определяем ординаты максимумов и минимумов
функции (анимация 1), затем их значения откладываем с противоположным знаком ( анимация 2). симметричным отражением относительно оси
абсцисс предыдущего графика.
Для того чтобы полученный график отобразить симметрично относительно оси OX, мы определяем ординаты максимумов и минимумов
функции (анимация 1), затем их значения откладываем с противоположным знаком ( анимация 2).
|

|
| Через полученные точки проводим искомую кривую синим цветом. |

|
Получим график функции 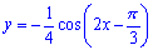 . .Построим итоговый график функции  , сдвигая пятый график на , сдвигая пятый график на
 вверх вдоль оси OY . вверх вдоль оси OY .
|

|
| Изобразим его красным цветом. Итак, мы построили график функции 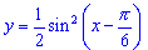 путем элементарных преобразований графика функции
y=cos x. путем элементарных преобразований графика функции
y=cos x. |

|
Элементарные преобразования функции 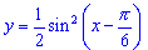 изображены разными цветами на одном графике. изображены разными цветами на одном графике.
|

|